西野友年『ゼロから学ぶベクトル解析』読了

本書全体の感想

本書の特徴は寒いギャグに違いないと思う．一例を紹介しよう

「オレはミリカン，飲み代はワリカン」(p.85)
「ランダウを恨んだ」(p.185)
「好物は，まず口に入れてから後悔せよ──ダイエットの第一法則だ．さあ食べよう．空海ゆかりの八十八ヶ所，デザート空海？そして後悔？」(p.170)

極寒の地，旅人が歩く．足裏の感覚はとうにない．食べ物を口にしたのはいつだったか？もうダメだ，そう思った，そのとき旅人は懐から本書を取り出し，一筋の希望を胸にページを捲った．すると──，
さらなる極寒が旅人を待ち受けていた.
そんな感じの寒いギャグが満載だ．恐ろしいのは読み進めるうちに著者のノリが僕に染ってしまったことだ（ここに，この文章に関係のある寒いギャグを入れる）．
こんなノリでベクトルという武器がない状態から，ざっくりとStokesの定理まで解説している（Greenの定理は積み残す）．著者が物理屋さんなので物理での適用例が豊富だ．というかそれしかない．あとがきによると，当初の予定ではNoetherの定理まで解説しようとしたけれど執筆一日目で諦めたそうだ．
個人的な本書の山場は6章「天才ガウスは帳尻合わせがお好き」にある，発散と体積分，ガウスの公式あたりの議論を何回か読みなおさないとストーリーが頭に入らなかったことと（説明自体はわかりやすい）,7章の後半で怒涛のように出てくる方程式（シュレディンガー方程式，湯川方程式，クライン・ゴルドン方程式，をいじったこと（ここらへん，ほとんど紹介だけに近い）．
なお，演習問題は殆ど無い．あとがきにもあるように「筋肉モリモリの教科書・参考書は売れない」からだろう．球面座標のラプラシアンも「教授に向かってそれができなきゃメシ抜きですとふっかけてみよう．「そんなの簡単だ！」と学生からの挑戦を受けておきながら，空腹のまま夕日を見る教授が多いだろう」として答えだけあげてある．
このようにチャランポランな感じがする著者だが，阪大物理科を主席で卒業しているあたりに世の不条理を感じざるを得ない．学生時代もこのノリだったのか？スーパーマンだ．そこに痺れる憧れる．

ゼロから学ぶベクトル解析 (ゼロから学ぶシリーズ)

作者: 西野友年
出版社/メーカー: 講談社
発売日: 2002/04/26
メディア: 単行本（ソフトカバー）
購入: 1人クリック: 31回
この商品を含むブログ (5件) を見る

内容はどう？

本書は電車内での通学時間に読むのに素敵に最適だ．ちなみに著者は次の本としてH.P.スウ『ベクトル解析』を挙げている．私も買いました．
ただ難点は，まあ数式が出てくると仕方ないのですが，誤植が多いこと（手元の本は初版1刷なのでさらに仕方ない．初版本は公式βテストだ）．図の座標のとり方が本文と違っていたり，一番ひどいところでは公式が間違えていたりする．例えば，

スカラー関数 $\phi(\mathbf{r})$ に対してrot divを取ると，必ずゼロになる．
$\textrm{rot div}\phi(\mathbf{r})=\nabla\times(\nabla\phi(\mathbf{r}))=\mathbf{0}$
(p.151)

なんていうのがある．そもそも左辺と真ん中の辺はノットイコールだ．計算すればわかるが，これはrot divではなくrot gradが正しい．なぜこんな誤植をしているのか謎だ．
著者のページを見ると，次に出す本は「興味ある高校生や、大学の新入生も手に取れる量子場の入門書」であるところの『今度こそわかる場の理論』（講談社）らしい．

疑問点

以降の記述は原書のpp.47-50に相当．特記されている箇所以外は，適宜私の言葉で省略してある．

位置ベクトルを用いて点Qでの高さをh( $\vec~q$ )と書くことにする．x-y直交座標系をとる．x,y軸方向の単位ベクトルをそれぞれ $\vec~e_x,\vec~e_y$ とする．
ある点Qから点Q'へのベクトルを $\Delta~\vec~q$ としよう．

(1)

点Aを点Qからx軸方向に⊿x=εcosθ進んだ点とする.

(2)

点Bを点Qからy軸方向に⊿y=εsinθ進んだ点とする．
（つまり，点Q'は点Qからx軸方向に⊿x=εcosθ，⊿y=εsinθ（θはx軸と $\Delta~\vec~q$ のなす角）進んだ点である．）

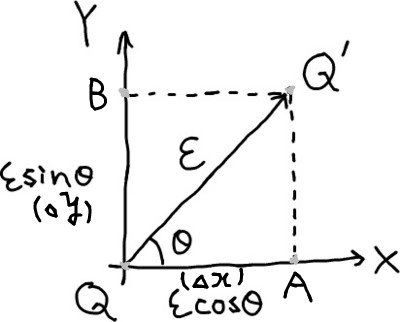
図1 Q'の位置
勾配を定義する．

Definition:勾配

$\frac{\Delta~h}{|\Delta~\vec~q|}\overset{\mathrm{def}}{\Longleftrightarrow}\frac{h(\vec~q+\Delta~\vec~q)-h(\vec~q)}{|\Delta~\vec~q|}$

εを十分に小さくとる（移動は微小）のものとする．QからQ'にかけての斜面は近似的に平面を傾けたものになる．
さて点Qから点Aへの登りは

(3)

$(\Delta~_xh\equiv){h(\vec~q+\Delta~x\vec~e_x)-h(\vec~q)}$
また，点Qから点Bへの登り*1は

(4)

$(\Delta~_yh\equiv){h(\vec~q+\Delta~y\vec~e_y)-h(\vec~q)}$

図2 「登りの分解」概念図
「進む距離と登った高さは（ほぼ）比例するから， $\Delta~_xh$ は⊿xに， $\Delta~_yh$ は⊿yに比例している．」（後述の疑問点で重要な箇所ゆえ原文のまま）
「ところで，もう一度図を見ると[注：図2はmotosoが書き直した別物]BからQ'に登る経路 $\bar{BQ'}$ は，OからAに登る経路 $\bar{OA}$ を平行移動したものだと一発で（？）わかるだろう．またBからQ'への登りも，OからAへの登りに等しい．」（括弧内は原文のまま．おそらく「OからA」は「QからA」の誤植．ただし元の図には原点Oがある．）よって，
$h(\vec~q+\Delta~x\vec~e_x+\Delta~y\vec~e_y)-h(\vec~q+\Delta~y\vec~e_y)\approx{h(\vec~q+\Delta~x\vec~e_x)-h(\vec~q)}$
これを使うとQからQ'への登り⊿hは次のようになる．
⊿h= $h(\vec~q+\Delta~x\vec~e_x+\Delta~y\vec~e_y)-h(\vec~q)$
= $h(\vec~q+\Delta~x\vec~e_x+\Delta~y\vec~e_y)-h(\vec~q+\Delta~y\vec~e_y)+h(\vec~q+\Delta~y\vec~e_y)-h(\vec~q)$
= $h(\vec~q+\Delta~x\vec~e_x)-h(\vec~q)+h(\vec~q+\Delta~y\vec~e_y)-h(\vec~q)$
= $\Delta~_xh+\Delta~_yh$
ここまではいい．図からも直感的に納得出来る（そもそもこの数式いじりは直感的にしか納得できないよねというアレやソレはおいておこう）．
さて，これを分配の定義式に入れよう．すると，
$\frac{\Delta~h}{|\Delta~\vec~q|}=\frac{h(\Delta~_xh+\Delta~_yh)}{|\Delta~\vec~q|}=\frac{\Delta~_xh}{\varepsilon}+\frac{\Delta~_yh}{\varepsilon}$
$=\frac{h(\vec~q+\varepsilon\cos\theta\vec~e_x)-h(\vec~q)}{\varepsilon}+\frac{h(\vec~q+\varepsilon\sin\theta\vec~e_y)-h(\vec~q)}{\varepsilon}$
ここもよい（(1)〜(4)式までを眺めれば分かる）．次が分からない．

「ここで $\Delta~_xh$ は $\Delta x$ に， $\Delta~_yh$ は $\Delta y$ に比例している量だったから， $\cos\theta$ や $\sin\theta$ をカッコの外に引っぱり出せて
$\frac{\Delta~h}{|\Delta~\vec~q|}=\cos\theta\biggl\{\frac{h(\vec~q+\varepsilon\vec~e_x)-h(\vec~q)}{\varepsilon}\biggr\}+\sin\theta\biggl\{\frac{h(\vec~q+\varepsilon\vec~e_y)-h(\vec~q)}{\varepsilon}\biggr\}$
と「X方向への勾配の $\cos\theta$ 倍」と「Y方向への勾配の $\sin\theta$ 倍」に分離できる。」（強調部は引用者による）
本書ではこの後すぐε→0の極限をとり偏微分を定義する．ここまでが一連の流れである．最後の強調部（カッコの外に引っ張り出す）はなぜ出来るのかが僕には不明だった（比例しているとできるの？）．なぜだろう．

解答

まず $\frac{\Delta~_xh}{\varepsilon}$ について考える．
$\frac{\Delta~_xh}{\varepsilon}=\frac{h(\vec~q+\varepsilon\cos\theta\vec~e_x)-h(\vec~q)}{\varepsilon}$
$=\frac{h(\vec~q+\varepsilon\cos\theta\vec~e_x)-h(\vec~q)}{\varepsilon\cos\theta}\cos\theta$
ここで $\varepsilon'=\varepsilon\cos\theta$ とおくと $\varepsilon\to 0$ のとき $\varepsilon'\to0$ だから
$=\left\{\frac{h(\vec~q+\varepsilon'\vec~e_x)-h(\vec~q)}{\varepsilon'}\right\}\cos\theta\;(\varepsilon\to 0)$
と， $\cos\theta$ を引っ張り出すことができる． $\frac{\Delta~_yh}{\varepsilon}$ についても同様．

分からなかった原因は？

$\varepsilon$ も $\varepsilon'$ も結局0に収束するので本書では同じ文字（ $\varepsilon$ ）で書いていて，ここが混乱の元だった．数学の先生に質問に行ったところ，数学ではこういう略し方をすることがあるとのこと（実はこの回答も僕が考えたのではなく，教わったのだ）．
ともかくこれで1年半ぶりに疑問がとけた．

別解（2012/03/05 1533）

「ここで $\Delta~_xh$ は $\Delta x$ に， $\Delta~_yh$ は $\Delta y$ に比例している量だったから， $\cos\theta$ や $\sin\theta$ をカッコの外に引っぱり出せて」の部分がまるっと使われていないことに気づいたので別解をば．まあやっていることは同じなんだけど．
$\Delta~_xh$ が $\Delta x$ に比例しているので，比例定数kを用いて
$\Delta~_xh=k\Delta x\cdots(1)$
$\Leftrightarrow k=\frac{\Delta~_xh}{\Delta x}$
$=\frac{\Delta~_xh}{\varepsilon\cos\theta}$
$=\frac{h(\vec~q+\varepsilon\cos\theta\vec~e_x)-h(\vec~q)}{\varepsilon\cos\theta}$
ここで $\varepsilon'=\varepsilon\cos\theta$ とおくと
$=\frac{h(\vec~q+\varepsilon'\vec~e_x)-h(\vec~q)}{\varepsilon'}$
$(1)/\varepsilon$ に代入して
$\frac{\Delta~_xh}{\varepsilon}=k\frac{\Delta x}{\varepsilon}$
$=\frac{h(\vec~q+\varepsilon'\vec~e_x)-h(\vec~q)}{\varepsilon'}\frac{\varepsilon\cos\theta}{\varepsilon}$
$=\frac{h(\vec~q+\varepsilon'\vec~e_x)-h(\vec~q)}{\varepsilon'}cos\theta$
以降は上と同様．